Simulación

Práctica 2: autómata celular

En la segunda práctica trabajamos con autómatas celulares [6] en dos dimensiones, particularmente el famoso juego de la vida [7]. El estado del autómata se representa con una matríz booleana (es decir, contiene ceros y unos). Cada celda es o viva (uno) o muerta (cero). En cada paso, la supervivencia de cada celda (verde) se determina a partir de los valores de sus ocho vecinos (amarillos):

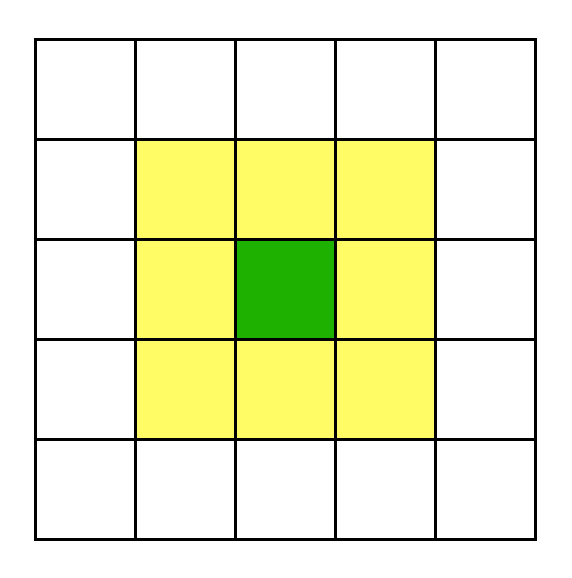
En los extremos de la matríz, las celdas simplemente tienen menos vecinos. (Otra alternativa sería considerar el espacio como un torus — pareciendo una dona — donde el extremo de abajo se reune con el extremo de arriba igual como los lados izquiero y derecho uno con otro.

La regla de supervivencia es sencilla: una celda está viva si exactamente tres vecinos suyos están vivos. Para comenzar, usamos números pseudoaleatorios como el estado inicial. En R se necesita el paquete sna para visualizar matrices de este tipo con facilidad, mientras en Python se necesita el paquete numpy además del matplotlib de la práctica anterior (requerda instalar una vez y cargar antes de cada uso).

• Código en R
• Código en Python

Tarea 2

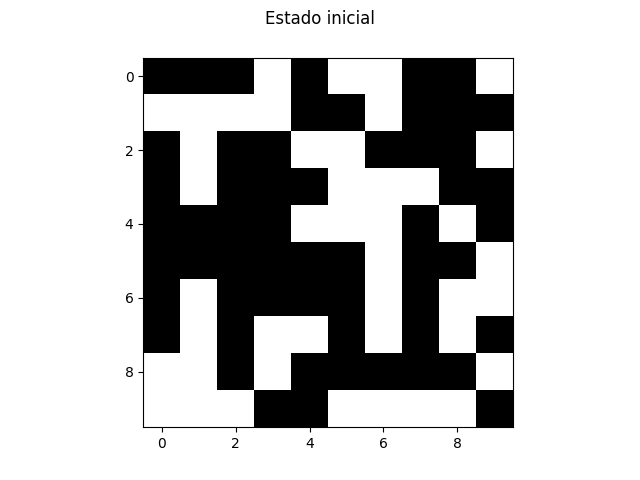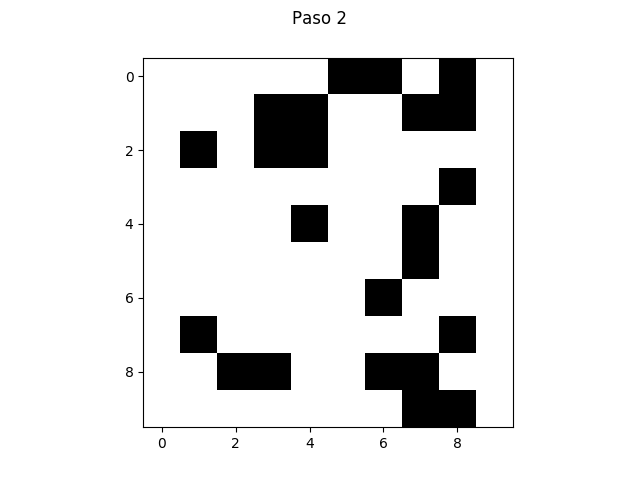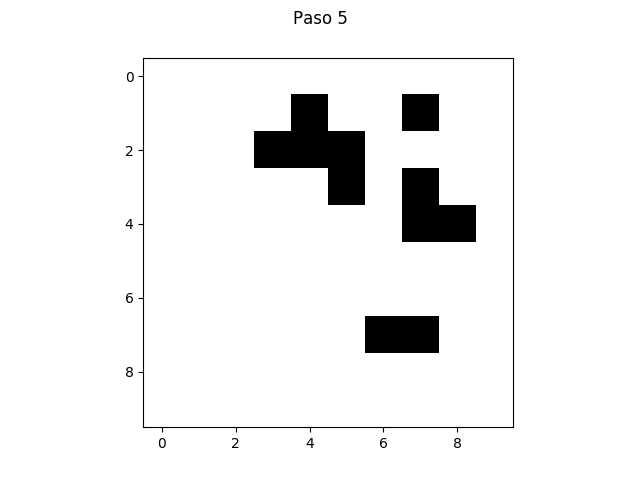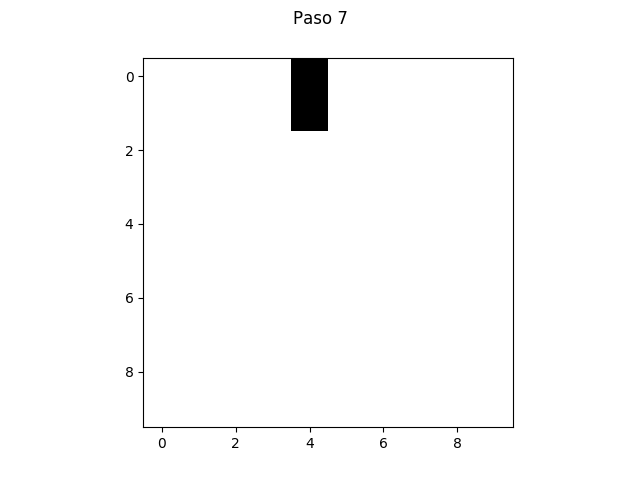
Diseña y ejecuta un experimento con por lo menos 30 réplicas para estimar la probabilidad de creación de vida dentro de 50 iteraciones (es decir, haya celdas vivas al final de la réplica), usando niveles 10, 15 y 20 para el tamaño de la malla y los niveles 0.2, 0.4, 0.6 y 0.8 para la probabilidad inicial de vida. Visualiza y tabula los hallazgos.

El primer reto es modificar la simulación para que modele algún tipo de crecimiento (o cristalización) en la microestructura de un material. Núcleos aparecen al azar en celdas desocupadas y expanden con una tasa constante a celdas vecinas hasta agotar el espacio disponible. Examina la distribución de los tamaños de los núcleos que no toquen el borde al finalizar la simulación, elegiendo el tamaño de la zona y el número de semillas de tal forma que sean por lo menos la mitad. Codifica las identidades de los núcleos como enteros y normaliza antes de dibujar la matríz para que los niveles de gris estén entre cero y uno como espera la rutina que los visualiza; también puedes utilizar palettes de colores, con que se distingan bien.

El segundo reto es ejecutar el un autómata celular en un modelo tri-dimensional, por ejemplo estos modelos; se puede visualizar archivos STL en en un servicio web. Si el modelo que quieres usar está en formato binario (es decir, no contiene texto), se convierte en formato ASCII usando un script de ruby con ruby convertSTL.rb modelo.stl donde el segundo argumento es el nombre del archivo del modelo STL por convertir, lo que produce un modelo-ascii.stl como resultado.

De la versión ASCII del modelo STL, se extrae un CSV con los normales y las tres esquinas con python3 ascii2csv.py Star.stl > Star.csv en el siguiente formato:

• las columnas 1, 2 y 3 representan el normal del triángulo,
• las columnas 4, 5 y 6 son la primera esquina,
• las columnas 7, 8 y 9 son las segunda esquina,
• las columnas 10, 11 y 12 con la tercera esquina.

En el reto, procesa a ese CSV en un data.frame de R o con pandas en Python: dos triángulos son vecinos si comparten dos esquinas, dando a cada triángulo un total de tres vecinos. Al inicio, cada celda está o prendida (TRUE) o apagada (FALSE), uniformemente al azar. Cada celda tomará el estado en el que se encuentra la mayoría de sus vecinos (sin contar a si mismo). Se proporciona una plantilla del esquema general en R:

input = "modelo.csv"
m = read.csv(input, header = FALSE) # modelo 3D
n = dim(m)[1] # cuantas celdas hay
init = runif(n) > 0.5 # estados iniciales, mitad prendidos
state = init
require("parallel")
cluster <- makeCluster(detectCores() - 1)
clusterExport(cluster, "m")
clusterExport(cluster, "n")
dur <- 5 # cuantos pasos
for (iter in 1:dur) {
    clusterExport(cluster, "state")
    state <- parSapply(cluster, 1:n, step) # el reto es implementar la rutina step
    print(".") # indicador de avance rudimentario
}
stopCluster(cluster)
m$state = state
write.table(m, "resultado.csv", sep=',', col.names = FALSE, row.names = FALSE) 

Agrega los estados de la última iteración como una nueva columna (la última) en el data.frame y guarda los datos en formato CSV como salida (la rutina agrega un contador en la primera columna), digamos resultado.csv. A este CSV se convierte de regreso a formato ASCII OBJ con python3 csv2obj.py resultado.csv > resultado.obj lo que se puede visualizar en otro servicio web. El ejemplo abajo muestra el estado inicial y la primera iteración para una esfera.