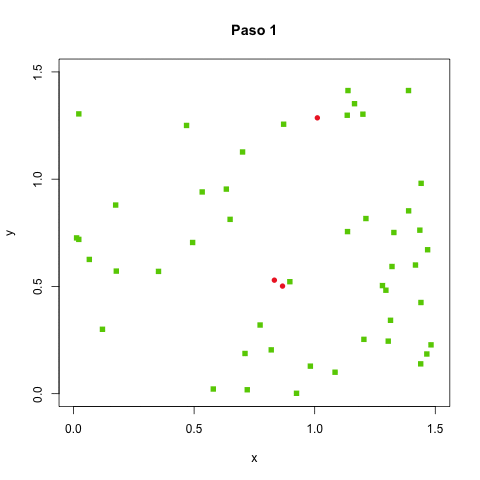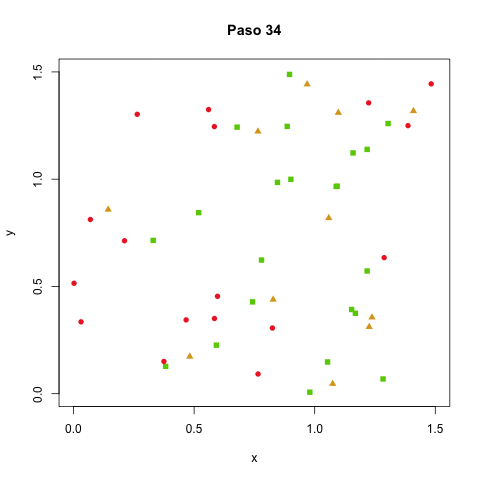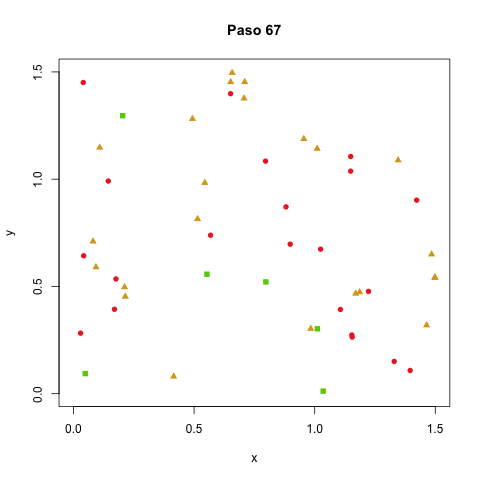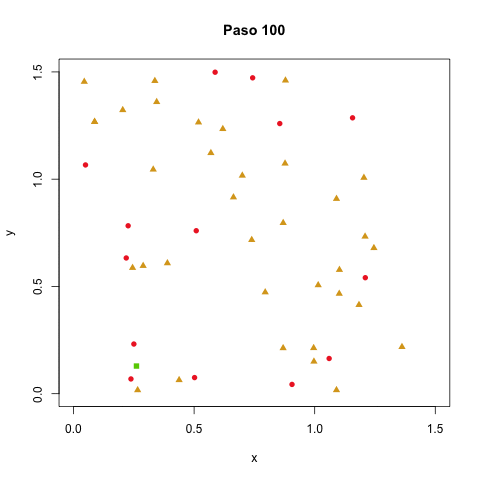
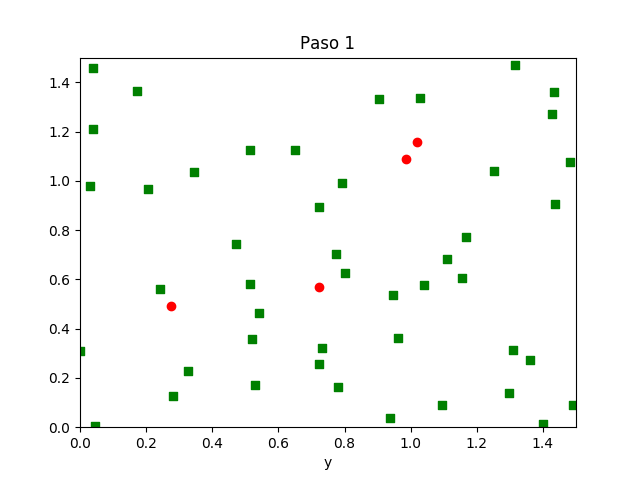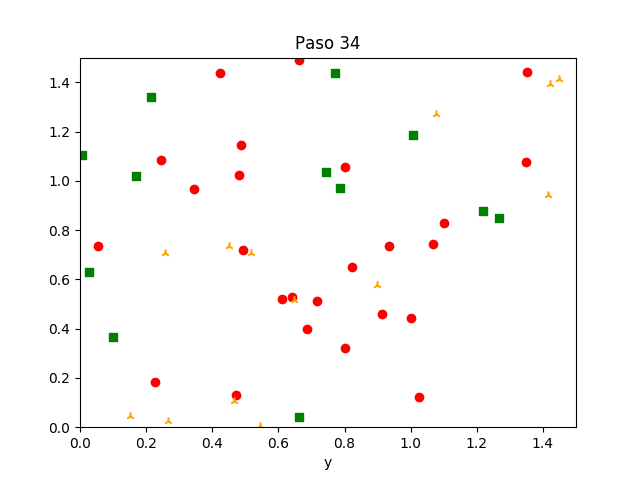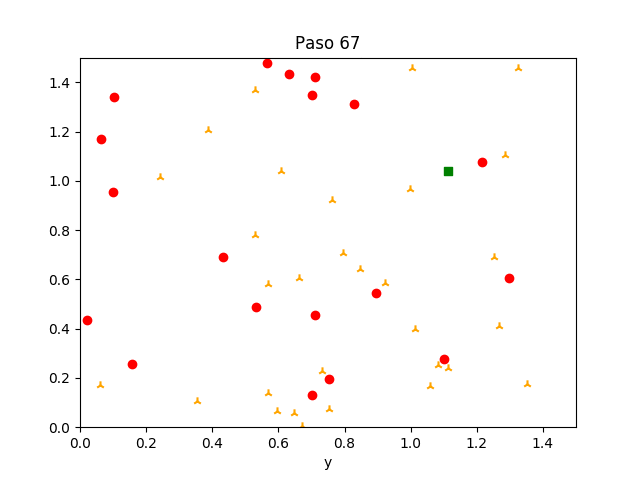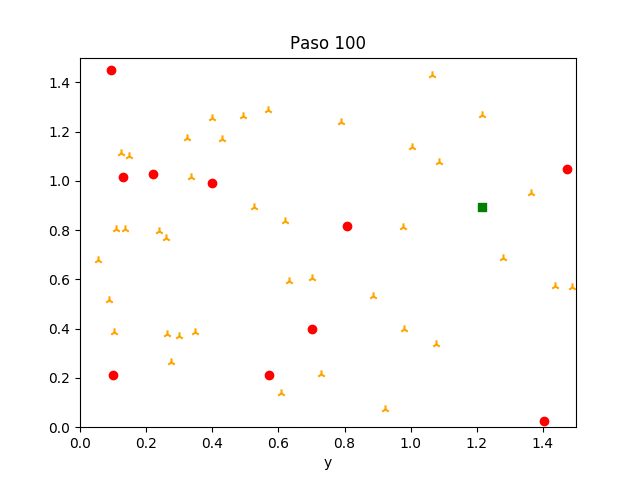
Un sistema multiagente es un poco como un autómata celular: hay un conjunto de entidades con estados internos que pueden observar estados de los otros y reaccionar cambiando su propio estado. La diferencia es que un sistema multiagente es un concepto más general y permite que estos agentes se muevan y varien su vecindad, entre otras cosas. En la sexta práctica vamos a implementar un sistema multiagente con una aplicación en epidemiología. Los agentes podrán estar en uno de tres estados: susceptibles, infectados o recuperados — esto se conoce como el modelo SIR.
Los parámetros serán el número de agentes $n$ y la probabilidad de infección al inicio $p_i$. Vamos a suponer, por simplicidad, que la infección produce inmunidad en los recuperados, por lo cual solamente los susceptibles podrán ser infectados. La probabilidad de contagio será en nuestro caso proporcional a la distancia euclideana entre dos agentes $d(i, j)$ de la siguiente manera:
$p_c = \left \{ \begin{array}{ll} 0, & \text{ si } d(i, j) \geq r, \\ \displaystyle\frac{r - d}{r}, & \text{ en otro caso,} \end{array} \right.$
donde $r$ es un umbral.
Nuestros agentes tendrán coordenadas $x$ y $y$, una dirección y una velocidad (expresadas las dos últimas simplemente en términos de $\Delta x$ y $\Delta y$). Vamos a posicionar los agentes, por ahora, uniformemente al azar en un torus formado por doblar un rectángulo de $\ell \times \ell$, visualizando en todo momento el rectángulo en dos dimensiones (lo de torus simplemente significa que arriba y abajo se juntan, igual como izquierda y derecha, así como en Pacman).
l <- 1
n <- 30
pi <- 0.05
v <- l / 20
agentes <- data.frame(x = double(), y = double(),
dx = double(), dy = double(),
estado = character())
for (i in 1:n) {
e <- "S"
if (runif(1) < pi) {
e <- "I"
}
agentes <- rbind(agentes, data.frame(x = runif(1, 0, l),
y = runif(1, 0, l),
dx = runif(1, -v, v),
dy = runif(1, -v, v),
estado = e))
}
l = 1 n = 30 pi = 0.05 v = l / 20 from random import random, uniform import pandas as pd # instalar con pip3 agentes = pd.DataFrame() agentes['x'] = [uniform(0, l) for i in range(n)] agentes['y'] = [uniform(0, l) for i in range(n)] agentes['dx'] = [uniform(-v, v) for i in range(n)] agentes['dy'] = [uniform(-v, v) for i in range(n)] agentes['estado'] = ["S" if random() > pi else "I" for i in range(n)]
Lo que se ocupa agregar es el cálculo de los contagios y el movimiento de los agentes.
Para seleccionar colores en R, conviene revisar un catálogo de los nombres disponibles.
En esos códigos, nadie se está recuperando aún. Agregamos que en cada paso, con probabilidad $p_r$, un agente infectado puede recuperarse y ya no volverse a infectar.
$ rm -f p6_t*.png # por si hay versiones anteriores
$ Rscript SIR.R
$ convert -delay 20 -size 300x300 p6_t*.png -loop 0 p6.gif
$ rm -f p6p_t*.png # por si hay versiones anteriores
$ python3 SIR.py
$ convert -delay 20 -size 300x300 p6p_t*.png -loop 0 p6p.gif
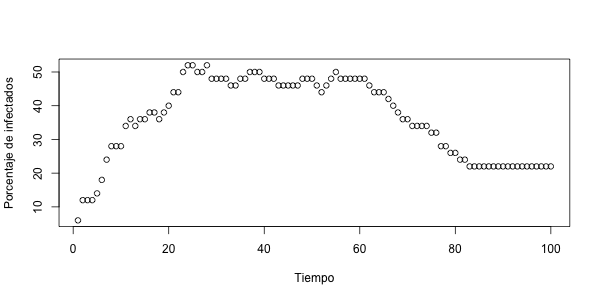
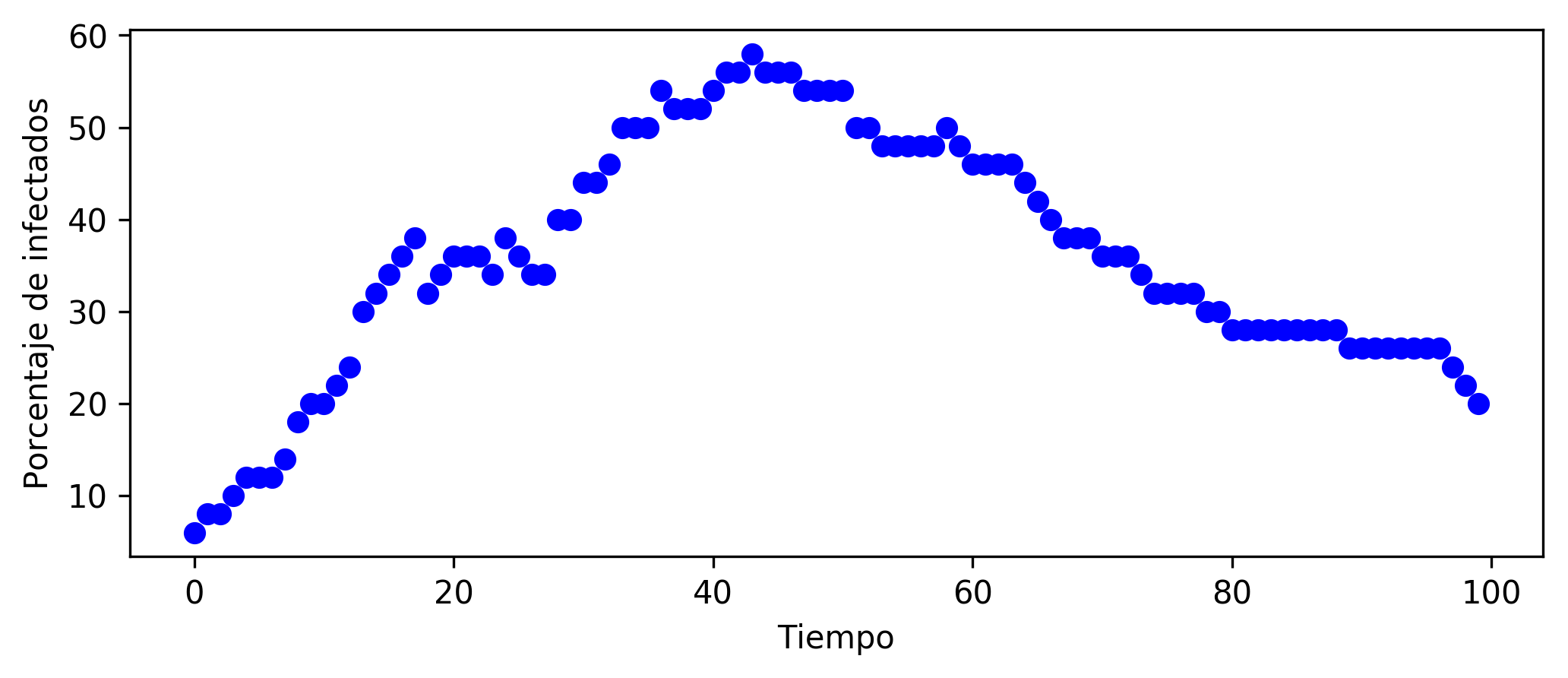
Estudia el efecto de "contención" en el sentido de que agentes infectados reduzcan su velocidad de movimiento a la mitad durante su infección. Determina con pruebas estadísticas adecuadas si este cambio produce un efecto significativo en la magnitud de la epidemia (la altura del pico en la curva del porcentaje de infectados por iteración) y en la velocidad de ella (la iteración en la cual se llega por la primera vez al valor pico).
En el primer reto, vacuna con probabilidad $p_v$ a los agentes al momento de crearlos de tal forma que están desde el inicio en el estado R y ya no podrán contagiarse ni propagar la infección. Estudia el efecto estadístico del valor de $p_v$ en (de cero a uno en pasos de 0.1) el porcentaje máximo de infectados durante la simulación y el momento (iteración) en el cual se alcanza ese máximo.
En el segundo reto, los agentes tienen amistades: si se encuentran una distancia euclideana no mayor a $r_a$ de un amigo suyo, se disminuyen su velocidad a la mitad por $k_a$ iteraciones (para saludar a su amigo). Cada par de agentes tiene una amistad con una probabilidad $p_a$. Examina nuevamente si surgieron cambios en el efecto de $p_v$ por esta modificación, con valores $0 < r_a < 1$, $k_a > 1$ y $0 < p_a \ll 1$ de tu elección.
https://satuelisa.github.io/